The Primary Colors of Phi
- Clay Taylor
- Oct 20, 2019
- 17 min read
This article is a continuation of my research project 1st detailed in my article “Light and Color Theory of the Electromagnetic Spectrum”, originally published in 2016. It is recommended that you begin with that article before continuing your journey here.
This work is dedicated to all geometers past and present, who have endeavored to capture the foundations of reason for the illumination of all.
LET THERE BE LIGHT
It may be argued that light is the most striking function of nature to the perception of mind among matter. We human beings know it best through the most sensitive of our miraculous biological instruments- our eyes. In opening our eyes to light, our reality is illuminated in its exquisite and dynamic detail, the feats of which are profound. Unlike our other senses which perceive our more immediate environment, through our sight we are able to receive and distinguish information from the very close and the very small, where the tips of needles terminate into so many atoms, on up to the incomprehensible distances where galaxies become one with vanishing points… We are clearly well equipped and well-tuned to our cosmos.
Of course, when we speak of “light” we must distinguish some parameters. Today, we know very well that “light” as electromagnetic waves, exist beyond the visible range of our eyes, which are tuned to receive barely a single octave of electromagnetic wavelengths nestled among the macro and microcosm before fading from our visual perceptions. This light is often depicted as a lonely rainbow among this greater spectrum which ascends and descends by orders of magnitude into the scales of the ineffable, where measurements have no further discernible meaning in our preferred quantifications of the universe.
To me, this narrow window of visible “light” conjures up comparisons to how our own vibrant planet is often envisaged, as Carl Sagan stated, a “pale blue dot… a mote of dust suspended in a sunbeam.” It is this sense of endless scale that leads to some modern convictions of the sort that limit the fundamental value of the scale of our planet, and of our light, in respects to the whole of the universe. How is there any more purpose to the dimensions of our planet, which is one of untold billions, than a single grain of sand upon the beach? What truth may the behaviors of one octave of electromagnetic radiation teach us, among a never-ending continuum? What significance is there in the one among the all?
But we are well tuned to our cosmos. We are not some mere statistic among eternity. We are natural law incarnate, seeing ourselves in the stability of our own measure. We are inertial- balanced in the dynamic stillness of the gravity of our miraculous orbit, where we find ourselves at temperate equilibrium, a “Goldilocks zone” of ideal thermodynamic exchange centering a supreme harmonic masterpiece that flames, freezes, radiates and absorbs itself into the tangible realm we feel and see before us.
Its clues are all around us.

It is in the spirit and the acknowledgement of this anthropic principle that I have continued to study the nature of the light in our inertial environment, for clues to the higher nature of the universe at large.
THE MYSTERY WITHIN THE SPECTRUM
In 2016, I published some of my early investigations into the geometric logic of color theory and electromagnetic refraction in my article “Light and Color Theory of the Electromagnetic Spectrum.”
I sought to understand the miraculous, almost too-good-to-be-true rules of color theory, and how these rules correlated to natural features of refraction through many varieties of prisms and other media (which also challenged the accuracy of other well-known theories of light refraction, such as those developed by Newton and Goethe.) This also led to the research project which I titled, “Spherical Refraction – The Magnetic Relationship Between Light and the Universal Shape.”
In each series of simple and unique experiments where I examined the behavior of light refraction as closely as I possibly could, I routinely measured extremely intriguing Phi constant mathematical/ geometric relationships, most notably between the primary colors Red, Green and Blue, and the secondary colors, Cyan, Magenta and Yellow.
I determined that in the refraction process of a continuous spectrum, 3 discrete beams are the principle output- the primary colors of Red, Green and Blue in the additive process, or conversely, the secondary yellow, magenta and cyan in the subtractive process. These 3 primary rays of light are projected from white unity in deviating angles, which then experience different combinations of one another to create the complete spectrum in accordance with the well-established color logic utilized in our modern technology.

Both the temporal frequencies and the spatial wavelengths of these 3 primary and secondary colors were distributed by the “golden ratio” Phi, which existed as the difference between the waves. It was also found in the ratio of their respective distances of dispersion.
While I believe it may be possible that I am the first to directly measure this relationship in refraction specifically, this fact was originally described by Jon DePew, a gifted magnetic researcher and inventor who has long discussed the broad role of Phi in magnetism, including its correspondence to the primary colors, and whose work largely inspired this very investigation. I believe Jon deserves credit for this discovery which I have sought to further study and elucidate.
RAYON VERT
The middle value of this relationship, which corresponds with the color green in the additive process (or the absence of the color green in the subtractive process which produces magenta), was particularly intriguing to me. I noticed an extremely synchronistic fact in that the wavelength and frequency that I had measured as the value of this center ray of refraction, was equal numerically to the square root of the speed of light in kilometers. This had the entirely one-of-a-kind result that its frequency in terahertz and its wavelength in nanometers were the same number and decimal, 547.53307…
In accordance with the speed of light formula, these two numbers multiply to the velocity of light, (or the rate of induction of electromagnetic waves.) In the grand scheme of the electromagnetic spectrum, this color was also extremely close to the peak wavelength of our sun. In the terms of human body, it is nearly identical to the peak sensitivity of the human eye and fit directly in the center of the average human range of visual perception as well. Furthermore, it strangely bound seemingly subjective units of Earth measure, the meter and the second, and our base ten/ decimal system of measure with the physical constant of light speed. What are the odds?! These were synchronicities I could not ignore.

Obviously, a profound mathematical and geometrical distributive order was unfolding out of the continuous spectrum of our sunlight which challenged a deep-seeded cultural belief system of random chance nature- it became obvious that somewhere within this accumulating information, a fundamental tenet of energy distribution was at work within the frequency and wavelength, or the timing and spacing of light speed, relative to our existent physical composition. It just so happens that our units of measurement and our ancient counting systems were well suited to compute this (as also evident by the mathemagic of phi based calculations as a whole.)
What was the scale of this Phi based color distribution? What else could be inferred by the synchronicities found in the center of the visible spectrum? This is where I continued my investigation.
A TALE OF TWO RATIOS
While I understand all ratios to be mathematically interrelated, if one were to ask me what I would consider to be the most fundamental ratios of all, my answer would be the Octave (doubling and halving) and Phi, represented by the symbol Φ. (It is assumed the reader is already familiar with the basics of these values.)
These two ratios are known to be related in ways that may be described geometrically, but in terms of the timing and spacing of vibrations, they are very practically opposites. The octave clearly exists in the realm of utterly rational whole numbers (1,2,4,8 and on) while Phi is considered “the most irrational number.” From one, it immediately strays from wholeness and no successive iteration of Phi (1.618…) will ever return to wholeness (unless of course, as the reader should be aware, it is multiplied by its counterpart, in this case phi, represented by the symbol φ, 0.618… which returns it to 1.)
In the realm of sound vibrations for instance, the Octave makes it clear that doubling and halving of a fundamental tone retains the tonal quality of that fundamental. Even while it now exists in a higher or lower pitch, it is in essence the same key which may be repeated to infinitely higher or lower intervals. Thus, the Octave is effectively the most harmonic interval possible. In contrast, a note that is a value of phi from that fundamental will never truly reach the original tonal quality of the root/ tonic/ fundamental reference tone, even within an eternity of iterations. Another way to imagine this is that if Phi rotated around a clock, starting at noon, due to its incommensurability it will never hit exactly noon ever again, no matter how many times you turned it by this value. In contrast, the Octave would hit 1:00 every single time (in its doubling direction.)

So here we have the most harmonic and resonant ratio of all as the octave, with completely static tonality. In terms of resonance, Phi is the opposite; it is the ultimate damping ratio. Structures built upon this ratio for instance will work to eliminate standing wave resonance. (I recommend the work of Richard Merrick, such as his book “Interference Theory” in exploring the damping concept further.)
It is conceivable that these two opposing functions are mutually requisite for a dynamic and stable universe; one where whole ratio harmonic resonance and stable standing waves may exist in all their splendor via the octave, yet may be given motion by an equally recursive mathematical constant fractal such as Phi. (I like to imagine that Phi and the Octave would be akin to the unstoppable force meeting the immovable object.)
These are compelling behavioral descriptions, but to me, the relationship between these key tenants of vibratory physics remained largely unexplained… I had actually long sought a more compelling mathematical reconciliation to how Phi and the Octave coexist.
SCALES OF LIGHT
So I found myself with 3 primary color wavelengths occupying a unique sliver of the vast electromagnetic spectrum… what did it mean in this practically endless expanse? These wavelengths unto themselves were not in phi proportions- it was the difference between them that contained the phi ratio. Why? What math constant values did these wavelengths directly correspond to in their own respect? Was the difference between them merely a coincidence? Furthermore, if these wavelengths were fret positions on an instrument, how would one place them in respect to the framed octave in the first place?

I decided to analyze these wavelengths within a triangle. The center line of the triangle would represent the “fundamental tone” of 1. The bottom length of the triangle would then equal the doubled Octave (being double the length of the middle line.) The tip of the triangle would then represent 0. Successive halving of the fundamental line in the center would unveil the structure of the inwardly recursive octave intervals. By setting the central refraction beam of green as the fundamental, I could let it equal 1; the red and blue wavelengths would then fit below and above green in relation.

I found I could convert the green 547.533 nanometer value to 1 by multiplying it by the wavelength’s “wavenumber” .001826373. This I would then set as the fundamental. Multiplying the red and blue wavelengths by the same value would leave their ratios intact and I could more easily discern their mathematical relationship relative to one. If there was a discernible constant relationship here, it could be more easily discovered- this was the case.
By setting the green wavelength to one, I essentially created a new unit of measurement. For lack of a better term, I call this the Clayton. This obviously led me to name the corresponding frequency unit of measure, equal to 547.533 terahertz, the Taylor. 1 Clayton, multiplied by 1 Taylor thus equaled the speed of light. This makes things much more comprehensible. From here on, all mathematical relationships will be in terms of Claytons and Taylors. The definitions of 1 Clayton and 1 Taylor are below:

THE PRIMARY COLORS OF THE PHI FUNCTION
It has been stated by researcher Jon DePew, that “Phi is much more than a number” (or its most popular iteration relative to one, I would add.) He says “it is better to look at Phi as a function- the process of dividing something equally.” For anyone who seriously studies Phi and its self-referencing behaviors mathematically, this becomes massively evident. Just take a quick look at some of its values I calculate below from several of its common geometric manifestations.

By setting the green wavelength to 1, I was easily able to determine that the value of the red wavelength was equal to 2φ, or 2/Φ, which is a value of 1.236… this is the” Harmonic Mean” of Phi! (Its own “octave” would be φ, or Φ-1.)
The Blue wavelength value was then determined to be most easily expressed as φ^3+φ, or 1-φ^4 with a value of .8541…
To complete the picture in Phi ratio terms, the green wavelength of 1 could of course be expressed as φΦ.

I was of course delighted to discover that by setting green to the value of one in this triangle, the octave relationships could not only be maintained, they retained a veritable explosion of phi ratio relationships all throughout the infinitely recursive scales towards 0!

There are many ways to express the same values in Phi and phi terms. On the left is phi (φ) variations, and on the right are some Phi (Φ) expressions.
The phi relationship can be seen to not just exist as the difference between the 3 wavelengths with green as the center; it is now also the difference between all their octaves, as well as between every variation of wavelength taken as the center, and finally, as their relationship to 0!


This, my friends, is how Phi coexists with the octave. For obvious reasons, I like to call them the primary colors of Phi. I backtracked my way to this discovery by studying light and color theory, of all things!
GEOMETRIC MANIFESTATIONS OF THE PRIMARY COLORS OF PHI
But how else do these “primary colors of Phi” fit into fundamental geometry, shapes and physics functions of the natural world? And through which other lenses may we view them, beyond the colors of our vision alone?
Here I show how these wavelengths would correspond relative to one another in the well-known Phi spiral. We see that each primary wavelength of refraction would fit directly into well establish geometric proportions of this famous shape.
Starting with green and red:
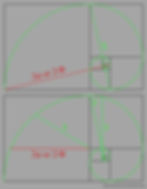
Here we see blue in respect to green:
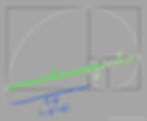
I might add here that while studying the 1-φ^4 mathematics (blue wavelength), I developed an equation that approximates the famous “Fine Structure Constant” to 99.96% accuracy with the CODATA recommended value. A coincidence perhaps, but strangely compelling, and I’d argue it’s among the most eloquent and simple equation approximations as well…

Continuing into the realm of spirals, I analyzed the “spiral decay ratios” of these 3 wavelength’s numerical values. The “spiral decay ratio” determines the curvature characteristics of a spiral- how much it bends, in which direction it bends, where it terminates etc. I will call it “SDR” for short.
The SDR for 1 (our green wavelength) turns out to be a circle. An SDR of our Red wavelength 2φ spirals outwardly from the circle of 1. An SDR of our blue wavelength 1-φ^4 spirals inside the circle. This very much reminds me of the physical dispersion of these primary colors away from one another in the refraction process.
This image shows these spirals mirrored for symmetry. Note how the spirals interact with one another’s octaves as well:

Of course, if we look at the higher octaves of these values, they will all spiral into the circle of 1. The octave of the circle itself would now represent the spiral of the Octave itself. Note how all the spirals terminate into one another.
In fact, when in relation to one another’s termination points, they seem to always hit their mark, like fractal vortexes…
Might I add, I did find this interesting... coincidence?

Φ'VE FOLD GEOMETRY
Moving on, the next obvious geometry to look at would be the 5-fold geometry of the pentagon/ pentagram, due to the well-established mathematics of Phi throughout.
I found that if the side of a pentagon was a length of the Green wavelength, the radius to the extreme point of the pentagram (or circumscribed circle) would be the blue wavelength. The red wavelength would then be represented as the ratio between the inscribed and circumscribed circles.

When it comes to tiling space, the pentagon is insufficient unto itself and 10-fold geometry is needed. Our wavelengths really explode in these geometries, which in my experience hint at their presence in 3 dimensions.
It was at this point that I turned my attention to the tiling of space.
THE QUASICRYSTALLINE TILING OF 5
It was clear to me that these phi values would play a prominent role in the tiling of 5-fold geometry. Tiling 5-fold geometry in 3 dimensions is the logic that governs what are known as quasicrystals; an aperiodic (irregular and non-repeating) crystallization pattern of physical matter.
Here we see the convergent beam electron diffraction pattern reveal the physical inner structure of one of these quasicrystals. What you are seeing is a 3d aperiodic physical crystal lattice projection in 2d perspective.

How would our primary wavelengths fit into this structure?
The answer is that we find these “primary colors of phi” are all throughout and practically formulate the underlying logic in the distribution of the particles in both 3 dimensions, and the 2d projected image!

There is so much to be found… Here I demonstrate that this structure encodes the ratio of phi unto itself at 90 degrees. (The phi ratios therein are at a ratio of 1 to ¾ to one another.)
This profoundly beautiful math corresponds precisely to both the physical structure, and the wave structure of our natural world.
Here I apply what I learned about the logic of these ratios to replicate a quasicrystal diffraction pattern from scratch:


The fact that this ratio tiling is perfectly retained in vanishing point perspective/ projective geometry is extremely compelling to me and speaks to a fundamental relationship of phi in 2 dimensions vs 3 dimensional projective geometry and physics. It is the logic of phi within the octave!


Linking this phi damping ratio to physical matter distribution is insightful to me in terms of matter creation. Again, “damping” in physics pertains to the tendency to restrain vibratory motion, such as mechanical oscillations, noise, and alternating electric currents, by the dissipation of energy. Naturally, this principle must be at work in stabilizing structures and particles, and in the allowance of steady states.
THE PRIMARY COLORS OF PHI AND MAGNETIC STABILITY
Both phi and the octave are principle ratios within all platonic solids, and this is equally true of icosahedrons and dodecahedrons. The 3-dimensional geometry of quasicrystals are composed of 3d tiling based upon icosahedral and dodecahedral forms, which when combined give the forms capable of tiling 3d space, such as the Rhombic Hexecontahedron and the Rhombic Triacontahedra and others, which must be combined in aperiodic fashion, much like Penrose tiling in 2d.
Notably, these structures are extremely magnetically stable (though this is not true of the dodecahedron unto itself.) Thus, as these phi functions we explore were discovered in the study of electromagnetic field refraction, they likewise can be found to be stable as magnetic structures.
Below are examples of icosahedral magnet configurations. While other platonic forms may display varying degrees of magnetic stability, the icosahedron seems to be among the most inert (the large shape on the left has sat on my desk for years and has not collapsed despite endless interference on my part.)


GOLDEN VIBRATIONS
We must remember that when dealing with the speed of light, all ratios we explore in terms of space pertain equally to terms of time. Fractal space is fractal time. So while we have been mainly exploring our primary wavelengths spatially, and in respect to aperiodic tiling of space, we now turn back to vibration and frequency.
In these time-based terms, aperiodic of course means the vibration is not cyclic and has no regular intervals- it is mathematically incommensurable.
In the graph below, I visualize the overlapping sin waves of the 3 frequencies and their cumulative aperiodic nature. Interestingly, at every point of overlap with the line of propagation, the phi ratio is maintained between the 3 waves, despite these positions continuously rearranging themselves in respect to one another. This is an incommensurable and aperiodic oscillation that maintains the Phi ratio in every single configuration of its pulses.

As we know, when red, green and blue light waves mix with one another, it is experienced as pure white light. It should be obvious now that white light in its most reducible form (as RGB) is a phi coded aperiodic electromagnetic frequency- a result of phi coexisting with the octave. As all secondary, tertiary colors and beyond are admixtures of the 3 primaries, it stands to reason that phi ratios beat aperiodically in any color combination from these sources.

THE PRIMARY COLORS OF PHI IN SPHERICAL REFRACTION
As I’ve already referenced, this research project into color theory and refraction had led me to investigate the behavior of light refraction upon a sphere. Some of this work I summarized in my article “Spherical Refraction – The Magnetic Relationship between Light and the Universal Shape.” In this project, I painstakingly mapped the geometry of all the refraction and reflection phenomena that results when sunlight strikes a transparent medium in the shape of a sphere.
This project revealed a wealth of interconnected mathematical beauty to say the least… putting it into words is practically futile, but I will try to break down some key elements.
Many math constants were found within- nearly every feature of reflection and refraction was found to be tied to a famous mathematical value. Ultimately, the geometry primarily seemed to embody the spatial interaction of Phi, the octave and the square root of 2.
To a physicist, the interaction of phi with the square root of 2 should imply the interaction of phi with the inverse square law, which is fundamental to the physics of vibrations, including light as electromagnetic waves. This returns us to the physics of projective geometry (light projecting through a sphere is of course a quintessential case of projective geometry.

Here we see the primary focal point of the sphere, where the sunlight collected upon half of the sphere focuses to a point a half-radius distance from the circumference of the sphere.

Here we see the "spectrum beams" which project from either end of the sphere. The large beam which points out in the direction of the incoming light from the opposite end of the sphere is equal in length to √2 of the diameter of the sphere. A Phi ratio exists between the difference of the diameter of the sphere and the length of this positive projection beam, and the diameter of the sphere to the length of the negative projection beam which aims back towards the sun. The value of the negative projection beam is Φ(√2-1)-1.
In addition to these notable features, we also find rainbow cones of light projecting out of each end of the sphere. The cone of refraction in the positive output direction (opposite end of sphere from incoming sunlight) is emitted at a circumference equal to 1-φ^4, our blue wavelength. On the input side of the sphere (where the sunlight strikes) is projected the negative opposing refraction cone aiming back towards the sun. This cone exits the sphere at a circumference equal to φ (which is the octave of our red wavelength with the value 2.)

Thus we have the primary colors of phi encoded into a higher order of proportion, in the geometry of spherical refraction.
Another prominent Phi based angle that plays a major role in this refraction geometry is that of the "Phi Scaling Angle." This is the angle which is produced by adding successive circles upon one another which increase at the Phi or phi proportions.

My friend and colleague Marshall Lefferts has done exceptional work to unveil the prevalence of this "Phi Scaling Angle" in the natural world, and to explore its reasoning within the geometry of the Phi function itself. I highly recommend Marshall's book "Cosmometry". It is a veritable compendium of important concepts which are highly complimentary to the information explored in this very article. You will even find this diagram printed within its pages.
Some of the features of this geometry is of course the reason for rainbows! If you imagine the sphere of glass is a bead of water vapor (water has nearly identical refractive index as glass and is transparent to light), the angles of the refractive cones aimed back towards the sun, inversely correspond to the angles at which you will see a rainbow, and a double rainbow (at between 40° towards blue and 42.5° towards red for the primary rainbow and 50° towards red, to 53° towards blue for a double rainbow respectively), relative to the shadow of your head (the "antisolar point"), with the sun directly behind you.

I have found that degree values within the range of each rainbow phenomena appear when our phi ratios are applied to degrees in a circle.
As I have also discussed in my article “Temple of Constants”, these angles of rainbow refraction are also the angles that define the geometry of the Great Pyramid of Giza (the side wall angle being 51.8° and the corner angle being 42° respectively.)
Here our study of light launches us into mankind’s greatest structural achievement of all time- our ancient miracle temple of mathematical constants and Earth measure.

Above we see the side view diagram of the Great Pyramid of Giza aligned with the rainbow refraction cone which projects back towards the sun. The peak of the pyramid touches middle green. The inversion of the cone would hit the sphere's center. The base of the pyramid would rest at the refraction cone circumference which is equal to φ of the sphere's diameter. Several other architectural features of the pyramid cross section seem to correspond to the other principle characteristics of the light refraction that are present.
The Great Pyramid of Giza, built upon units of measure harmonically proportioned with the Earth, Moon and Sun, angles itself in a manner which synchronistically unites the proportionalities of the fundamental mathematical constant relationships, and is now shown to come to its peak at a point that defines the central wavelength of human vision and the peak wavelength of our sun at its central refraction angle, as projected from transparent matter.

I can think of no greater, and no more beautiful of a miracle- as if god’s golden green smile winks at us in every ray of sunlight- with the mathematics of creation.
And thus we have learned of the primary colors of phi. We have seen that these ratios play a hidden role in coloring our existence- that they are bound both to the fundamental logic of math, and to the resultant geometries of lightspeed at work in our manifest reality- as manifestations of recursive phi damping within the octaves of the electromagnetic spectrum.
Continue on to Part 3- THE PROPORTIONS OF ILLUMINATION.
#Phi #phi #electromagnetism #magnetism #light #color #colorlogic #octave #quasicrystals #phitiling #primarycolors #colortheory #geometry #sacredgeometry #pyramid #giza #greatpyramid #green #squaredcircle #goldenratio #base10 #claytaylor #phispiral #spiral #pentagon #pentagram #damping #sphere #refraction #rainbow #antisolarpoint






























































































































































